Investigación Análisis de Redes

 

Formulación de Modelos de Programación Lineal

Elementos básicos de un modelo matemático

Un modelo matemático es producto de la abstracción de un sistema real, eliminando las complejidades y haciendo suposiciones pertinentes; se aplica una técnica matemática y se obtiene una representación simbólica del mismo.

Un modelo matemático consta al menos de tres elementos o condiciones básicas: Las Variables de decisión, la Función Objetivo y las Restricciones.

Variables de decisión y parámetros

Las variables de decisión son incógnitas que deben ser determinadas a partir de la solución del modelo. Los parámetros representan los valores conocidos del sistema o que se pueden controlar. Las variables de decisión se representan por: X1, X2, X3,…, Xn ó Xi, i = 1, 2, 3,…, n.

Función Objetivo

La función objetivo es una relación matemática entre las variables de decisión, parámetros y una magnitud que representa el objetivo o producto del sistema. Es la medición de la efectividad del Modelo formulado en función de las variables. Determina lo que se va optimizar (Maximizar o Minimizar).

La solución ÓPTIMA se obtiene cuando el valor de la Función Objetivo es óptimo (valor máximo o mínimo), para un conjunto de valores factibles de las variables. Es decir, hay que reemplazar las variables obtenidas X1, X2, X3,…, Xn; en la Función Objetivo Z = f (C1X1, C2X2, C3X3,…, CnXn) sujeto a las restricciones del modelo matemático.

Por ejemplo, si el objetivo es minimizar los costos de operación, la función objetivo debe expresar la relación entre el costo y las variables de decisión, siendo el resultado el menor costo de las soluciones factibles obtenidas.

Restricciones

Las restricciones son relaciones entre las variables de decisión y los recursos disponibles. Las restricciones del modelo limitan el valor de las variables de decisión. Se generan cuando los recursos disponibles son limitados.

En el Modelo se incluye, adicionalmente de las restricciones, la Restricción de No Negatividad de las Variables de decisión, o sea: Xi = 0.

/*La programación lineal es la interrelación de los componentes de un sistema, en términos matemáticos, ya sea en forma de ecuaciones o inecuaciones lineales llamado Modelo de Programación Lineal. Es una técnica utilizada para desarrollar modelos matemáticos, diseñada para optimizar el uso de los recursos limitados en una empresa u organización.

El Modelo de Programación Lineal, es una representación simbólica de la realidad que se estudia, o del problema que se va a solucionar. Se forma con expresiones de lógicas matemáticas, conteniendo términos que significan contribuciones: a la utilidad (con máximo) o al costo (con mínimo) en la Función Objetivo del modelo. Y al consumo de recursos disponibles (con desigualdades = ó = e igualdades =) en las restricciones. */

Problemas de aplicación para formular un modelo

1). Proceso de producción.- Una fábrica produce dos tipos de productos: M y N, los costos de producción de ambos productos son $3 para el producto M y $5 para el producto N. El tiempo total de producción está restringido a 500 horas; y los tiempos de producción son de 8 horas/unidad para el producto M y de 4 horas/unidad para el producto N. Formule el Modelo matemático que permita determinar la cantidad de productos M y N a producir, y que optimice el Costo total de producción de los dos productos.

Formulación del Modelo

En la formulación del modelo, podemos ayudarnos con la representación del Problema mediante un organizador gráfico o esquema.

El método gráfico se emplea para resolver problemas que presentan sólo 2 variables de decisión. El procedimiento consiste en trazar las ecuaciones de las restricciones en un eje de coordenadas X1, X2 para tratar de identificar el área de soluciones factibles (soluciones que cumplen con todas las restricciones).

Para resolver un problema utilizando el método simplex es necesario que se maximice una función objetivo lineal sujeta a restricciones lineales que pueden ser de tipo igualdad o desigualdad. De forma matricial genérica del problema se podría plantear de la siguiente forma: Maximizar CTX (función objetivo).

Su área de aplicación es muy amplia, puesto que, se puede utilizar para resolver problemas de diversas disciplinas como son: finanzas, economía, mercadotecnia, logística, sistemas de producción, sistemas de transporte, entre otras.

El problema del transporte o distribución, es un problema de redes especial en programación lineal que se funda en la necesidad de llevar unidades de un punto específico llamado fuente u origen hacia otro punto específico llamado destino.

El problema

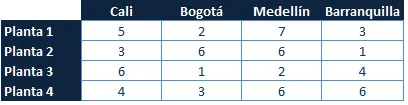
Una empresa energética colombiana dispone de cuatro plantas de generación para satisfacer la demanda diaria eléctrica en cuatro ciudades, Cali, Bogotá, Medellín y Barranquilla. Las plantas 1,2,3 y 4 pueden satisfacer 80, 30, 60 y 45 millones de KW al día respectivamente. Las necesidades de las ciudades de Cali, Bogotá, Medellín y Barranquilla son de 70, 40, 70 y 35 millones de Kw al día respectivamente. Los costos asociados al envío de suministro energético por cada millón de KW entre cada planta y cada ciudad son los registrados en la siguiente tabla.

Como ya lo hemos planteado en módulos anteriores el primer paso corresponde a la definición de las variables, regularmente se le denomina a las variables de manera algebraica Xi,j donde i simboliza a la fuente y j simboliza al destino. En este caso i define el conjunto {Planta 1, Planta 2, Planta 3 y Planta 4}, y j define el conjunto {Cali, Bogotá, Medellín y Barranquilla}. Sin embargo es práctico renombrar cada fuente y destino por un número respectivo, por ende la variable X1,2 corresponde a la cantidad de millones de KW enviados diariamente de la Planta 1 a la ciudad de Bogotá.

 

El segundo paso corresponde a la formulación de las restricciones de oferta y demanda, cuya cantidad se encuentra determinada por el factor entre fuentes y destinos, en este caso 16 restricciones.

Restricciones de oferta o disponibilidad, las cuales son de signo ≤:

X1,1 + X1,2 + X1,3 + X1,4 ≤ 80

X2,1 + X2,2 + X2,3 + X2,4 ≤ 30

X3,1 + X3,2 + X3,3 + X3,4 ≤ 60

X4,1 + X4,2 + X4,3 + X4,4 ≤ 45

Restricciones de demanda, las cuales son de signo ≥:

X1,1 + X2,1 + X3,1 + X4,1 ≥ 70

X1,2 + X2,2 + X3,2 + X4,2 ≥ 40

X1,3 + X2,3 + X3,3 + X4,3 ≥ 70

X1,4 + X2,4 + X3,4 + X4,4 ≥ 35

Luego se procede a formular la función objetivo, en la cual se relaciona el costo correspondiente a cada ruta.

ZMIN = 5X1,1 + 2X1,2 + 7X1,3 + 3X1,4 + 3X2,1 + 6X2,2 + 6X2,3 + 1X2,4 + 6X3,1 + 1X3,2 + 2X3,3 + 4X3,4 + 4X4,1 + 3X4,2 + 6X4,3 + 6X4,4

Luego se puede proceder al uso de la herramienta WinQSB para resolver el modelo realizado, aquí están los resultados.

Este problema presenta una solución óptima alternativa, aquí los resultados.

 

Red solución:

Los análisis de dualidad y sensibilidad en los modelos de transporte resultan ser bastante interesantes, pues pueden llegar a determinar aumentos de capacidad en las fuentes si el precio sombra de las rutas en relación a ellas lo justifica.

En general el problema de asignación es un problema de transporte equilibrado en el que suministros y demandas son iguales a 1, Así, un problema de asignación se caracteriza porque se conoce el costo de asignar cada punto de suministro a cada punto de demanda.

El Problema del Camino más Corto (o ruta más barata) consiste en encontrar una ruta o camino óptimo entre un nodo fuente y un nodo destino, los cuales están enlazados a través de una red con arcos que poseen un cierto atributo, el cual puede ser costo, distancia, tiempo, etc.

Algoritmo de DIJKSTRA

Tendremos a lo largo de todo el proceso dos conjuntos y dos vectores:

• Conjunto C : Conjunto de vértices candidatos. Inicialmente contiene todos los nodos menos el nodo origen.
• Conjunto S : Conjunto de vértices seleccionados, es decir, aquellos para los que ya conocemos su camino mínimo desde el nodo origen. Inicialmente contiene el nodo origen.
• Vector D : Almacenará la longitud del camino más corto desde el origen a cada nodo. Tendrá tantas posiciones como nodos tenga el grafo. El coste de ir del nodo origen a sí mismo lo estimaremos como cero.
• Vector P : Almacenará el nodo predecesor a cada nodo en el camino más corto desde el origen hasta él. Tendrá tantas posiciones como nodos tenga el grafo. La posición del nodo predecesor al origen estableceremos que sea cero para indicar que es el nodo origen.
• Llamaremos al nodo origen o, y el coste de ir del nodo i al nodo j lo denotaremos como COSTEij .

Hay que seguir los siguientes pasos: 

• Seleccionamos el nodo que sea destino de la arista con menor valor que salga del nodo o, llamémoslo u. Introducimos el nodo u en S y lo sacamos de C. Almacenamos en la posición u del vector D el valor COSTEou y en la posición u del vector P el valor del nodo predecesor, es decir, o.
• Seleccionamos el siguiente nodo al que podamos llegar con menor coste, bien directamente desde o, bien a través del otro nodo seleccionado u. Llamamos al nuevo nodo seleccionado v. Introducimos el nodo v en S y lo sacamos de C. Introducimos en la posición v del vector D el coste de llegar al nodo v, si es directamente desde o será COSTEov, si es a través de u será D[u]+COSTEuv. Por último, en la posición v del vector P introducimos el valor del nodo predecesor, ya sea o o u.
• Repetiremos este proceso hasta que todos los nodos hayan sido seleccionados, es decir, hasta que el conjunto C esté vacío, o lo que es lo mismo, hasta que en el conjunto S se encuentren todos los nodos del grafo. En ese momento en el vector D tendremos almacenado el coste mínimo para llegar desde el nodo origen a cualquier nodo del grafo, y podremos obtener el camino más corto mediante el vector P.

Ejemplo: Aplicar el algoritmo de Dijkstra sobre el siguiente grafo siendo el nodo origen el 1:

 

 

Los métodos CPM (método de la ruta critica o del camino critico, critical path method) y PERT (técnica de evaluación y revisión de programa, program evaluation and riview technique), se basan en redes y tiene por objeto auxiliar en la planeación, programación y control de proyectos. Se define un proyecto como un conjunto de actividades interrelacionadas, en la que cada actividad consume tiempo y recursos. El objetivo del CPM y PERT es contar con un método analítico para programar las actividades.

Para elaborar un diagrama CPM que incluya todo lo necesario, hay que seguir unas pautas. Gracias a ellas se podrá ver claramente el estado, evolución y previsión del proyecto en todo momento. Toma nota de cada paso a seguir.

Identificar y enumerar las actividades

Antes de elaborar el CPM es necesario identificar las actividades. Las cruciales serán las que no pueden atrasarse ya que, si sucede, se atrasará todo el proyecto. Por tanto, es imprescindible agruparlas en una lista y tener presentes en todo momento.

Identificar la dependencia entre actividades y ordenarlas

En este paso, previo a dibujar un diagrama de red, se debe detectar la dependencia y secuencia de actividades de dentro del proyecto. Para ello, es necesario identificar aquellas actividades que pueden realizarse paralelamente y cuáles dependerán de otras.

Dibujar un diagrama de red

Se puede hacer sobre papel o a través de diferentes programas de gestión de proyectos. Y como hemos mencionado anteriormente, en el CPM cada actividad empieza con un nodo o evento. Estos nodos están conectados a través de flechas, que representan las actividades que se deben completar para finalizar la tarea. Es por eso que, a través de softwares o herramientas online, a ti y tu equipo de trabajo os resultará más fácil de dibujar.

Establecer una duración aproximada por cada actividad

Hay que hacer una estimación del tiempo que va tardar en realizarse cada actividad. Aunque es una desventaja, se puede recopilar la información a través de los puntos anteriores, además de hablarlo con las personas implicadas.

Identificar la ruta crítica

Después de identificar las actividades, así como sus secuencias y duración, se puede calcular la ruta crítica. Para ello se deben utilizar 4 parámetros:

• Inicio optimista. Cuando la actividad anterior esté completada, se puede calcular el tiempo u hora que comenzará la siguiente tarea.
• Fin optimista. Hace referencia a la hora de inicio optimista + el tiempo que se haya necesitado para completar la actividad.
• Fin pesimista. Se refiere a la hora más tardana posible o el tiempo máximo al que se puede terminar una actividad sin que el proyecto se atrase.
• Inicio pesimista. Se calcula restando la hora de fin pesimista y el tiempo que se ha necesitado para completar la actividad.

Modificar el CPM, si es necesario

Como se trabaja con estimaciones, seguramente sea necesario actualizar el diagrama de CPM durante todo el proceso. De esta manera, se podrá saber si el proyecto va por el buen camino. Ahora bien, estos cambios afectarán a ala ruta crítica preestablecida, apareciendo otra de nueva.

La programación no lineal es un método por el cual se optimiza, ya sea maximizando o minimizando, una función objetivo. Esto, tomando en cuenta distintas restricciones dadas. Se caracteriza porque la función objetivo, o alguna de las restricciones, pueden ser no lineales.